RL knowledge List {.collection-title}
Name Tags keypoints
Value of the action W1_MAB Value of action = expected reward when the action is taken, q * (a) are defined as the expectedreward R_t from the action A_t but q*(a) we dont know→ we need to estimate it
Sample-Average Method W1_MAB Q_t(a) are defined as (sum of rewards when a taken prior to t)/(number of times a taken prior to t),
the doctor example W1_MAB As the doctor observe more patients, the estimated approach the true action value (**the sample average method**)
Action Selection W1_MAB The greedy action → they think it currently is the best! → has the largest estimated action value The agent is trying to get the most reward it can!
Balance W1_MAB short-term reward: choose greedy action → gamma = 0, not thinking about future at all long term reward: choose non-greedy action→ sacrifice immediate reward→ hopping to get more information about other actions → gamma = 1, thinking about future gamma: discount factor
Exploration- exploitation Dilemma W1_MAB conflict? balance?
Estimate action value incrementally W1_MAB Web advertisement problem
Incremental Update Rule Q_n+1 ⇒ 1/n * Sum(Ri)| i = 1 to n ⇒ 1/n *(R_n+ Sum(Ri)| i = 1 to n-1) Q_n+1 = Q_n + ( Rn -Q_n)/n**New Estimate ← Old Estimate + StepSize (Target -OldEstimate)*
Non- stationery Bandit Problem W1_MAB ???
What is the Trade Off W1_MAB Exploration: improve knowledge for long term benefit Exploitation: exploit short term benefit WE can not do both simultaneously
Epsilon-Greedy Action Selection W1_MAB ROLL a DICE epsilon: the possibility of choosing to explore
Optimistic Initial Values W1_MAB encourage exploration in early steps
Upper Confidence Bound Action Selection W1_MAB UCB = Upper Confidence Bound Use to decide the Action Selection Process,**betweenExploration&ExploitationHow UCB action-selection usesuncertaintyinestimationto drive exploration**
The difference of MAB and MDP W2_MDP MAB: same situation at each time→ single state→ the same action is always optimal MDP: different situation→ different response→ action chosen affect the amount of reward we can get into the future
Example W2_MDP Bandit algorithm tells a policy(which treatment to choose) for each trial. If he choose the sub optimalmedicine (i.e., performance of the medicine is less than other one) to treat the patient, then the cumulative performance will decrease. Unlike bandit, In MDP when you take an action, you will be in different state. MAB = MDP with**singlestateSituation = state, the action A_t change the state in MDP, create a new state St+1**
What is MDP? W2_MDP carrot / other vegetable , but different situation calls for different reactions carrot(lion) think about long term impact of our decisions
How to represent the dynamics of an MDP W2_MDP dynamics , transition dynamics from one state → to another
Formalization of MDP W2_MDP MDP formalization is flexible and abstract. \ states can be low level abstraction or high level abstractions, so it can be usde in various usages. (e.g. pixels, or object description in a photo) * time step can be short or very large
What’s the relationship of MDP and RL? W2_MDP RL : solve control task or prediction task MDP: sequential decision making problems, forma lize a wide range of this problems
RL W2_MDP RL: the goal for the agent is to maximize the future reward describe how the reward are related to the goal of the agent: long term goal, reward and future motion Returen Gt are defined as R_t+1 + R_t+2 + R_t+3 +… E(G) =E (sum(R…..)) maximize the expected Return → should be finite
identify episodic tasks W2_MDP naturally breaks into chucks called episodes each episode begins independently of how the previous one ends. e.g. Chess Game
What is a Reward Hypothesis? W2_MDP maximize the expected value expected future retuen That all of what we mean by goals and purposes can be well thought of as maximization of the expected value of the cumulative sum of a received scalar signal****(reward). Goals and purpose can be thought of as the maximization of the expected value of the cumulative sum of scalar rewards received
Continuing Tasks W2_MDP
Examples of Episodic and continuing tasks W2_MDP Epsodic: chess game regardless of how the game end, the new game states indepently
W2 summary W2_MDP MDP can formalize all problems in RL { State, Action, Rewards} Long term consequences, Actin → Future States + Rewards The Goal of RL: maximize**Total future reward → balance immediate reward with long term actions expected discounted sum of future rewards*
Discount W2_MDP 0<gamma <1 , the return remains finite gamma → 1, care about short term reward gamma→0 , we care about long term reward
Solve RL W2_MDP first step → MDP problems
Value Functions, Bellman Equations W3_Policy&Belman Once the problem is formulated as an MDP, finding theoptimal policy is more efficient when using value functions. This week, you will learn the definition of policies and value functions, as well as Bellman equations, which is the key technology that all of our algorithms will use.
Policy W3_Policy&Belman choose an action → reward + next state A policy is a distribution over actions for each possible state.
stochastic and deterministic policy W3_Policy&Belman Deterministic Policy: A Policy maps each states to a single action.**probability of 1** Policy(s) = a, States = s0, s1, s2 ; Actions = a0, a1, a2 (use Pie) Pi(s0) → a1, Pi(s1)→a0, Pi(s2)→a0. of course you can have same action for different state. In general, a policy assigns possibility to each action in each state. Pi(a|s) → represent a probability of selection of action a in state S Stochastic Policy: multi action be selected with non zero probability distribution → select actions in state S.**The stochastic policy might take the same step as the deterministic policy did.→ reach the Goal. Exploration/Exploitation trade-off (Epsilon greedy): can be useful for exploration**
generate examples of valide policies for MDP W3_Policy&Belman It is important that Policy only depends on the current state, not on thetime and previous state Valid policies:You don’t know about previous state anymore!!!!**You dont knowtime! Invalide Policies:The action depends on **something other than the state
Summary W3_Policy&Belman A policy maps**the current state**onto a set of possibilities for taking each action Policy only depends on the current state
Value Functions W3_Policy&Belman Delayed Reward: short term gain / long term gain? How to get a policy that achieve the most reward in the long term run? → Value Function is introduced to solve this issue.
Describe the role of state value/ action value function W3_Policy&Belman State Value Function: v(s) are defined as Expectation of (Future Reward an agent can expect to receive stating from a particular state) Action Value Function q_pi(s,a) are defined as Expected_pi (G_t | S_t =S, A_t = a) Value function predict rewards into the future
the relation between value functions and policies W3_Policy&Belman action, state, policy
examples of valid value function for a given MDP W3_Policy&Belman Chess game Reward : win +1; draw or loss 0 (not enough information to tell us how to achieve the goal) Value Function: Value V_pi(s) → probability for winning if we follow current policy Pi, at the current state
Bellman equation W3_Policy&Belman value of state and its possible successor derive Bellman equation ← state value function / action value function Understand how Bellman equation relates →**current and future values V_pi(s) are defined as the E_pi (Gt| St = s)** and G_t = R_t + gamma \ G_t+1
Why Bellman equation W3_Policy&Belman we can only directly solve small DMP problems use Bellman equation, possible to solve chess problems, scale up to large problems
Optimal Policies W3_Policy&Belman Policy→ how an agent behave → Value Function What’s the goal of RL: We want to find the best policy in the long run! How to find → we can get different Value on different Policy →In some state, Policy had different value→ pi(1) ≥pi(2) iff line 1 isabove line 2 An optimal policy**PI*is that italways has the highest possible valuein every state. There’s alwaysat least one Optimal policy( maybe more)Proof: Pi(3) = Pi(1) , Pi(2) , Optimal → pi *⇒ alwasy exist optimal policy!!!!
How to find Optimal policy W3_Policy&Belman simple question→ Brute Force Search complex→how to optimize the search in the policy space?→ Bellman Optimality Equations
W3 Summary W3_Policy&Belman what is a policy→ current state → tell an agent how to behave determinate: map sate → an action stochastic: map each state to a probability distribution value function on States and Actions, probability to win
The optimal state-value function: W3_Policy&Belman **Is unique in every finite MDP The Bellman optimality equation is actually a system of equations, one for each state, so if there are N states, then there are N equations in N unknowns. If the dynamics of the environment are known, then in principle one can solve this system of equations for the optimal value function using any one of a variety of methods for solving systems of nonlinear equations. All optimal policies share the same optimal state-value function.
What is DP W4_DP Dynamic Programming function p can be used to solve Policy evaluation and Control problem
Policy Evaluation & Control W4_DP distinction between policy evaluation and control Control ⇒task of finding a policy to obtain as much as possible DP problems use Bellman equations to defineiterative algorithms for both policy evaluation and control
Policy Evaluation W4_DP How good pi is? → pi → V_pi pi, p,gamma → DP → v_pi optimal policy! Control task complete iff current policy = optimal policy V_pi → policy evaluation pi * → control algorithms → compute value → DP
Iterative Policy Evaluation W4_DP DP are working as turning Bellman Equation intoupdate rules. First algorithm in DP → Iterative Policy Algorithms equation → iterative → get a approximate value → closer and closer to the value function(updated rule)Each iterationS → Sweep →v_pi V_pi is the unique solution to the bellman Equations
Policy Improvements W4_DP
Policy Iteration W4_DP You randomly select a policy and find value function corresponding to it , then find a new (improved) policy based on the previous value function, and so on this will lead to optimal policy
sequential decision making problem W2_MDPsocrative Long-term goal are generally more importantthan short-term consequences Agent does not always know completely the state of the environment e.g., partial observable problems
MDP W2_MDPsocrative State Space Action Space One-Step Dynamics In continuing tasks the discount factor must be smaller than 1
Explain briefly what is the reward hypothesis W2_MDPsocrative The reward hypothesis says that the agent is going to maximize the value of expected value of the cumulative sum of the received reward on the current state
Bellman Expectation Equations W2_MDPsocrative allows to evaluate a policy might be computationaly infeasible for large problems requires the knowledge of one step dynamics
Why DP W4_DPsocrative solving MDP is not easy
Define sweep in Iterative Policy Evaluation socrative first we have an initial step to estimation the value of the policy, then we use an iterative approach to update an estimation for the policy evaluation function, So we have a V’_pi to update the V_pi value at eachk step**for all states = at eachiteration of the algorithm, itupdates the value functionfor all the states , it“sweeps” through the state spaceof the problem**
Untitled
Slides Review {.collection-title}
Name Tags Keypoints
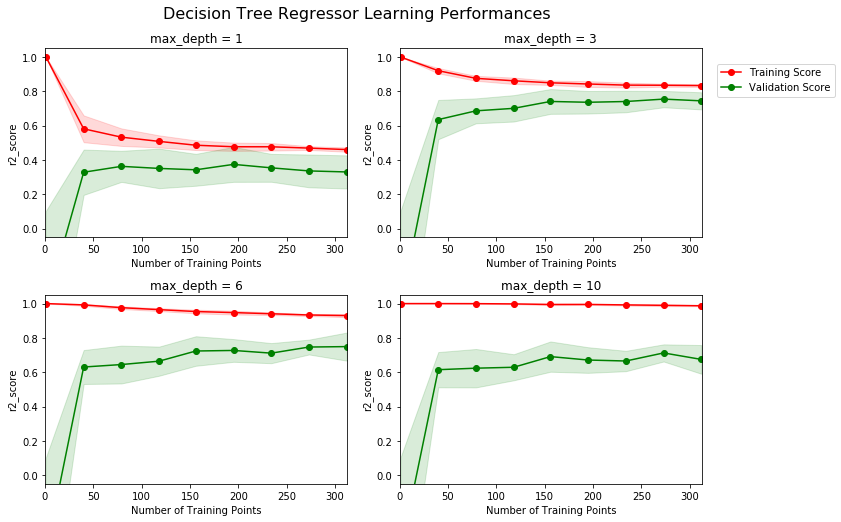
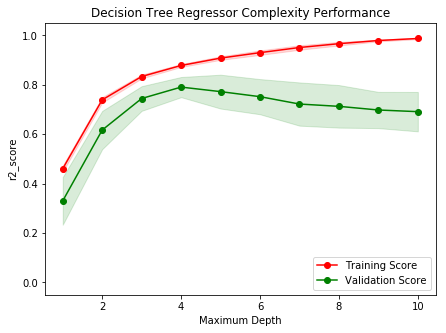
Bias-Variance Tradeoff 05_ModelEvaluation/Selection How to evaluate a model, can not use loss function The Bias-Variance is a framework to analyze the performance of models. 1. variancemeasures the difference between each model learned from a particular dataset and what we expect to learn. More sample / simpler model → decrease Variance 2. bias measures the difference betweentruth (𝑓) and what we expect to learn: more complex model→ decrease Bias
Model Assessment 05_ModelEvaluation/Selection high variance : under fitting high bias: overfitting low bias, low variance: good !
Regularization and Bias-Variance 05_ModelEvaluation/Selection The Bias-Variance decomposition explains why regularization allows to improve the error on unseen data.**Lasso outperforms Ridge regression when few features are related to the output*
Training Error/Prediction Error 05_ModelEvaluation/Selection Training Error: t_n-y(x_n) Prediction Error: (t_n-y(x_n)) \ p(x,t)
In practice 05_ModelEvaluation/Selection 1. Split randomly data into a training set and test set 2. Optimize model parameters using the training set 3. Estimate the prediction error using the test set high bias:training error is close to test error but they are both higher than expected high variance:training error is smaller than expected and it slowly approaches the test error
data split 05_ModelEvaluation/Selection Training Data → train model get parameter Validation Data→ validation error → select model with validation step → Test Data to estimate prediction error → raise 2 problems 1. enough validation data → less training data 2. overfitting ? How to solve ⇒ Cross Validation LOOCV ( lower bias but expensive to compute)/K-Fold cross validation (split in to K-folds, little bias, cheaper to compute)
How to choose the model 05_ModelEvaluation/Selection Reducing the variance choose right feature: the most effective subset of all the possible features dimensional reduction:lower- dimensional space Regularization: the values of the parameters are shrunked toward zero
No free lunch Theorems 05_ModelEvaluation/Selection Your favourite learner will not be always the best!
Feature Selection 05_ModelEvaluation/Selection AIC, BIC, AdjusterR2, etc. Cross-Validation
Dimensionality reduction 05_ModelEvaluation/Selection ⚠️Principal Component Analysis (PCA) P38**Dimensionality reduction aims at reducing the dimensions of input space, but it differs from feature selection in two major respects: it uses all the features and maps them into a lower-dimensionality space it is an unsupervised approach!*
Bagging and Boosting 05_ModelEvaluation/Selection \ Bootstrap Aggregation= Bagging(自主聚合)→ decrease high variance → suitable foe learner that is low bias and high variance/ overfitting problem ← bagging is suitable to decrease variance*** Boosting: high bias, the learner is not good enough ← need to fix it, boosting !!!!!!! → decrease bias/ still use simple learner/ keep the same variance (* still using weak learners: decision trees …) AdaBoost
VC dimension???? 06_LearningTheory ⚠️VC dimension
Kernel Ridge Regression 07_KernalMethods 看图片分布辨别用什么方法,linear/kernel
Kernel Design 07_KernalMethods
Kernel Regression 07_KernalMethods
Kernel Trick 07_KernalMethods can be used in …. Ridge Regression K-NN Regression Perceptron (Nonlinear) PCA Support Vector Machines … even Generative Models
What is MAB? 13_MAB Multi-arm bandit! far-sighted: gamma exploration/exploitation
different categories 13_MAB - Determistic - Stochastic { frequentist MAB , Bayesian }**-Adversarial Infinite time horizon: need to explore to gather more informationto find the best overall actionFinite time horizon: need tominimize short term lossbecauseuncertainty**
real example 13_MAB clinic test on new treatments! game playing slot machine Oil drilling new/unexplored/best/optimal
epsilon greeedy 13_MAB 1-e → greedy, instant reward; e → explore
softmax 13_MAB Weights the actions according to its estimated value Q(a|s) τ is a temperature parameter which decreases over time Even if these algorithms converge to the optimal choice, we do not know how much we lose during the learning process
MDP -relate to - MAB 13_MAB MDP → special case ( when the sate is single) → MAB State, Arm , Transition Matrix, Reward Function, discount factor(0< gamma <1 ), initial probability(optimistic estimation)
Goal 13_MAB maximize expectation value also minimize regret
Formulation 13_MAB 1. Frequentist formulation R(a1), . . . R(aN ) are unknown parameters A policy selects at each time step an arm based on the observation history 2. Bayesian formulation R(a1), . . . R(aN ) are random variables withprior distributions f1,…,fN A policy selects at each time step an arm based on the observation history and**on the provided priors**
Optimism in face of Uncertainty 13_MAB uncertain → explore→ get information & some loss in short term
Upper confidence Bound Approach 13_MAB ⭐️statistic approach → get a balance between exploration and exploitationthe bound length Bt(ai) depends on how much information we have on an arm, i.e., the number of times we pulled that arm so far Nt(ai)
UCB1 13_MAB ⭐️!!!!!!!!
Thompson Sampling 13_MAB 😇Pull the arm a with the highest sampled value Updatethe prior incorporating the new information Thompson Sampling → a method to solve MAB problem →optimal balance about explore/ exploit 1. sample from distribution to generate reward estimate 2. pick the arm with highest expectation 3. apply the arm and observe the reward 4. update distribution
EXP3 13_MAB 💥Variation of the Softmax algorithm Probability of choosing an arm,
Why DP 10_DP in order to find optimal policy of RL problem formulated in MDP, we need to find algorithms to evaluate policy value For small MDP problem→we can use brute force search For bigger MDP problem → DP can be used Dynamic Programming (DP) is a method that allow to solve a complex problem by breaking it down into**simpler sub-problems in a recursive manner** + Bellman Equation→ finite→unique Optimal solution→ pi*
Policy Evaluation 10_DP
Policy Improvement 10_DP
Policy Iteration 10_DP
Generalized Policy Iteration 10_DP
Efficiency of DP 10_DP
Untitled 12_TDL
What is supervised learning 02_SL It is the most popular and well established learning paradigm Data from an unknown function that maps an input 𝑥 to an output Goal: learn a good approximation of 𝑓 Classification if 𝑡 is discrete Regression if 𝑡 is continuous feature→ target Probability estimation if 𝑡 is a probability
When to apply supervised learning? 02_SL when human cannot perform the task When human can perform the task but cannot explain how When the task changes over time user-specific
overview 02_SL Define a loss function L Choose thehypothesis space H Find in H an approximation h of 𝑓 that minimizes L
Elements 02_SL Representation → Model Evaluation → Model selection Optimization →
Optimization 02_SL Combinatorial optimization e.g.: Greedy search ❑ Convex optimization e.g.: Gradient descent ❑ Constrained optimization e.g.: Linear programming
Parametric vs Nonparametric 02_SL Parametric:**fixed and finite number of parameters** Nonparametric: the number of parameters depends on the training set
Frequentist vs Bayesian 02_SL Frequentist: use probabilities to model the sampling processBayesian: use probability to model uncertainty about the estimate
Linear Regression 03_LR
Least Squares 03_LR
Regularization 03_LR
Least Squares and Maximum Likelihood 03_LR
Linear Classification 04_LC Learn, from a dataset 𝒟, an approximation of function 𝑓 𝑥 that maps input 𝑥 to a discrete class*𝐶 (with k = 1,…,𝐾)
Multi-class 04_LC In a multi-class problem we have K classes ❑ One-versus-the-rest approach uses K-1 binary cassifiers (i.e., that solve a two-class problem) each classifier discriminates 𝐶 and not 𝐶 regions ambiguity: region mapped to several classes ❑ One-versus-one approach uses K(K-1)/2 class binary classifiers each classifier discriminates between 𝐶 and 𝐶 𝑖𝑖 similary ambiguity of previous approach
hypothesis space 06_LearningTheory A hypothesis h is consistent with a training dataset 𝒟 of the concept c if and only if h(x) = c(x) for each training sample in 𝒟
VC Dimension 06_LearningTheory VC Dimension We define a dichotomy of a set S of instances as a partition of S into two disjoint subsets, i.e., labeling each instance in S as positive or negative ❑ We say that a set of instances S is shattered by hypothesis space H if and only if for every dichotomy of S there exists some hypothesis in H consistent with this dichotomy ❑ The Vapnik-Chervonenkis dimension, VC(H), of hypothesis space H over instance space X, is the largest finite subset of X shattered by H
Kernel Methods 07_KernalMethods Kernel methods allow to makelinear models work in nonlinear settings by mapping data tohigher dimensionswhere it exhibits linear patterns
Kernel in 1d example 07_KernalMethods linear separable
Kernel Functions 07_KernalMethods The kernel function is defined as the scalar product between the feature vectors of two data samples: Kernel function is symmetric:𝑘x,x′ =𝑘x′,x
sample-based methods 11_MonteCarlo With Dynamic Programming we are able to find theoptimal value function and the corresponding optimal policy
First-Visit & Evey-Visit 11_MonteCarlo Diff
Prediction & Control 11_MonteCarlo Diff Prediction: is to based on fixed policy to find maximize the estimation value of cumulated sum value. The input involves the policy Pi and MDP formulation. The output is the v_pi and q_pi Control: is to find be policy to achieve the goal, the policy is not fixed. The input is MDP description, and the output is the q_pi, V_pi, and Pi *(the optimal policy)
On-Policy & Off-Policy 11_MonteCarlo Diff policy iteration → how to get the Pivalue?
MC (Prediction and Control) 11_MonteCarlo Monte Carlo
diff between DP and MC 11_MonteCarlo ??
Valid Kernel 07_KernalMethods From the Mercers theorem, any continuous, symmetric, positive semi-definite kernel function can be expressed as a dot product in a high-dimensional space.
Rigid Regression, Logistic regression, Lasso Example What is it?
SVC sample Example 10^num_paramter, e.g. 100 = 10ˆ2
VC dimension Example
GMM Example GMM considers differently each dimension, by considering a generic covariance matrix while estimating the Gaussian distributions.
PARAMETRIC/NON–PARAMETRIC Example the difference
Q-learning Example what is q learning?